常见矩阵有哪些类型？如何根据需求选择合适的矩阵？

矩阵是数学中一个重要且广泛应用的工具，它在各个领域都发挥着重要的作用。在这篇文章中，我们将介绍一些常见的矩阵类型，并讨论它们在实际问题中的应用。通过了解这些常见的矩阵类型，读者将能够更好地选择适合自己需求的矩阵类型。

1.正交矩阵：保持向量长度和角度不变的特殊矩阵

正交矩阵是一个非常有用的类型，它在图像处理、信号处理和旋转变换等领域中得到广泛应用。正交矩阵的定义和性质使得它能够实现线性变换而不改变向量长度和角度。

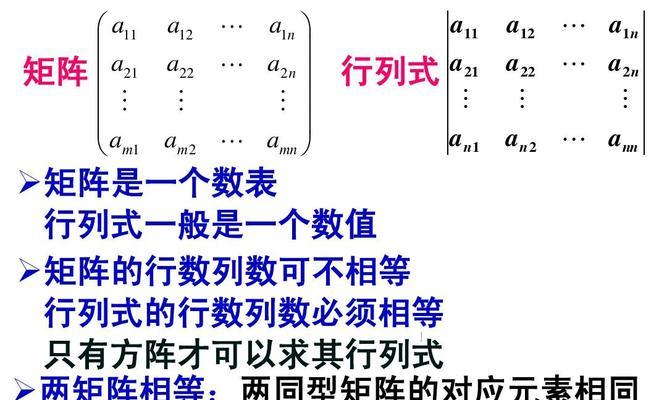
2.对称矩阵：重要的特征值性质与实对称矩阵的对角化

对称矩阵是一种具有特殊性质的矩阵，它的特征向量可以构成一组正交基。对称矩阵在物理学、机械工程和网络分析等领域中都有广泛的应用，例如在有限元分析中求解结构问题时，对称矩阵的性质能够大大简化计算。

3.上三角矩阵：简化线性方程组求解的关键

上三角矩阵是一种特殊的矩阵类型，它的主对角线以下的元素都为零。上三角矩阵在求解线性方程组时非常有用，因为它具有简化计算的性质。

4.对角矩阵：利用特殊结构进行高效计算

对角矩阵是一种所有非主对角线上元素都为零的矩阵。由于其特殊的结构，对角矩阵在矩阵乘法和求逆运算等方面具有高效计算的优势。

5.奇异矩阵：重要的性质与应用限制

奇异矩阵是一类特殊的矩阵，它的行列式为零。奇异矩阵在线性方程组求解和图像压缩等问题中有着重要的应用，但其奇异性质也限制了它的应用范围。

6.雅可比矩阵：在数值计算中的重要角色

雅可比矩阵是一种特殊的方阵，它在数值计算中起着重要的角色。雅可比矩阵常用于求解非线性方程组和优化问题，它能够通过迭代方法近似求解复杂的数值计算问题。

7.切比雪夫矩阵：多项式插值和逼近的利器

切比雪夫矩阵是一类特殊的矩阵，它与切比雪夫多项式密切相关。切比雪夫矩阵在多项式插值和逼近问题中具有很好的性质，能够提供高精度和稳定的结果。

8.希尔伯特矩阵：在数值分析和优化中的挑战

希尔伯特矩阵是一种特殊的矩阵，它的元素满足特定的规律。希尔伯特矩阵在数值分析和优化问题中常常被用作测试和挑战，由于其特殊结构带来的数值稳定性问题，求解希尔伯特矩阵的问题往往比较困难。

9.齐次坐标矩阵：计算几何和图形学中的重要工具

齐次坐标矩阵是一种在计算几何和图形学中广泛应用的矩阵类型。齐次坐标矩阵能够将欧氏空间中的点和向量转化为齐次坐标，从而简化了对几何变换的表示和计算。

10.稀疏矩阵：在大规模问题中节省存储和计算资源

稀疏矩阵是一种具有大部分元素为零的矩阵，它在处理大规模问题时能够节省存储和计算资源。稀疏矩阵在网络分析、图像处理和科学计算等领域中有着广泛的应用。

11.傅里叶矩阵：信号处理中的频域变换

傅里叶矩阵是一种与傅里叶变换相关的特殊矩阵，它在信号处理中起着重要的作用。傅里叶矩阵能够将信号从时域转换为频域，从而方便地进行频谱分析和滤波操作。

12.特征矩阵：特征值和特征向量的重要工具

特征矩阵是与给定矩阵具有相同特征多项式的方阵。特征矩阵能够帮助我们求解特征值和特征向量，这在物理学、工程学和金融学等领域中有着广泛的应用。

13.常对角矩阵：简化常微分方程组的求解

常对角矩阵是一种主对角线上的元素都相等的特殊矩阵。常对角矩阵在常微分方程组的求解中非常有用，因为它能够将一组耦合的微分方程分解为一系列独立的方程。

14.帕斯卡矩阵：组合数学和概率统计中的工具

帕斯卡矩阵是一种具有特殊结构的二项式系数矩阵，它在组合数学和概率统计中有着重要的应用。帕斯卡矩阵能够帮助我们计算组合数、求解概率分布和分析随机过程等。

15.非负矩阵：在数据分析和机器学习中的应用

非负矩阵是一种所有元素都非负的矩阵，它在数据分析和机器学习中有着广泛的应用。非负矩阵能够有效地处理非负数据，例如图像处理、文本挖掘和社交网络分析等问题。

通过本文的介绍，我们了解了常见的矩阵类型及其在实际问题中的应用。选择适合自己需求的矩阵类型能够提高计算效率和准确性，同时为解决具体问题提供了更好的工具和方法。无论是从正交矩阵到对角矩阵，还是从稀疏矩阵到非负矩阵，每种矩阵类型都有其独特的特性和应用场景，读者可以根据具体问题的需求选择合适的矩阵类型。